Perturbations of liquid curtains near break-up.
N. Legrand, P. Brunet, J.-M. Flesselles* and L. Limat
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH),
Ecole Supérieure de Physique et de Chimie Industrielles (ESPCI),
10 rue Vauquelin, 75005 Paris, France.
*present address: Saint-Gobain Recherches, 93303 Aubervilliers Cedex, France
Abstract
Experiments involving holes or sinuous waves are performed on silicon oil curtains falling between two guides from a horizontal tube (the slot being placed above or below the tube). Very near break-up, i.e. when the curtain contains a rather large subsonic domain for sinuous wave propagation, unusual states are observed: parabolic shaped holes formed below an obstacle, oscillating holes with liquid detachment from their edge, chessboard patterns of sinuous waves...
Though now an old subject [1], the stability of vertical liquid curtains remains a puzzling problem [1-6]. Available theoretical studies [2-4] always lead to the introduction of a Weber number We
=rhu2/(2g) that depends on the vertical co-ordinate z, and is built upon surface tension g, mass density r, local curtain thickness h(z), and local fluid velocity u(z). The curtain is supposed to be locally stable when We>1, and unstable when We<1. This criterion can be qualitatively established by two very different arguments:- A transient hole is imagined in the curtain at a position z [1]. Its apex is pulled from above by a force per unit length 2
g and "pushed" in the opposite direction by a momentum flux rhu2. When We>1 momentum dominates, the hole is convected downwards and disappears, while in the opposite case it growths upstream, invading the curtain.- The break-up is also often understood [2-4] as resulting from sinuous waves that are travelling at a velocity 
in a framework moving with the fluid. When c > u, these waves can propagate upstream, destabilising the curtain, the instability condition being again given by We<1. This argument has been renewed in terms of absolute and convective instabilities of open flows [3-4].
In practical situations this criterion appears to be of very poor help. The global stability criterion of the whole curtain remains disputed [5,6]: does one have to write the local criterion at the top of the curtain or at the base? In addition, patents indicate that a pronounced maximum of stability is obtained for a viscosity of order 30 cP, though the criterion upon Weber number is independent of the viscosity [5]. Indeed, recent theoretical analyses carried in terms of sinuous wave propagation, conclude that viscosity should be of negligible influence [3-4]. Clearly, careful experiments on curtains very near break-up are necessary to solve this puzzling situation. We present here preliminary results obtained in this direction. Though we will not solve the above paradox, we think that our observations constitute interesting indications for future studies.
A horizontal tube with a long thin slot (thickness e=2 mm) drilled along a generating line is supplied at its two ends with silicon oil at a constant rate Q. The oil flows across the slot and falls below the tube forming the curtain reproduced on Fig. 1, of typical width L=25.5 cm and height H=25 cm. By rotating the tube, the slot can be oriented downward or upward to change the boundary conditions in z=0, i.e. just below the tube. Curtain shrinking is prevented by two guides that are here two thin threads stretched by two weights. Several silicon oils Rhodorsil from Rhône-Poulenc are used of different viscosities (
h=10, 30, 50 cP, surface tension about g=20 mN/m). Visualisation of the curtains are performed by a high speed video camera, the curtains being lighten by reflection with a diffuse light.We have deliberately worked with relatively low flow rates per unit length
G=Q/L ranging between 0.5 and 2 cm2s-1. For both orientation of the slot, this leads to a fluid velocity nearly given by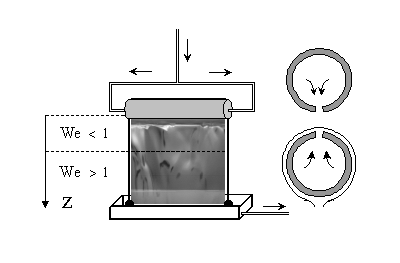
when z becomes larger than 1 cm or of the same order. In terms of sinuous wave propagation, the situation is that suggested on Fig. 1: a semi-infinite supersonic domain (We>1, i.e. c<u) and a subsonic strip (We <1, c>u), separated by what we will call a trans-sonic line where u=c. We here shortly report two set of experiments performed on these curtains. In the first set (section 3), the slot is oriented downward and the curtain is perturbed by a needle applied perpendicularly to the curtain at a controlled position z0 of local Weber number W0. Depending on the wetting properties of the needle, we are able to break the curtain or to perturb its lateral position without breaking. This allows us to compare more precisely the behaviour of holes and of sinuous perturbations, that are invoked in the two arguments recalled in section 1.
Figure 1: Sketch of the experiment. The curtain is falling from a horizontal slotted tube and guided between two vertical threads. As suggested on the right, the slot can be oriented downward or upward.
In the second set of experiments (section 4), the slot is oriented upward and we let the curtain destabilise by itself without applying any perturbation.
We have reproduced on figure 2 several images obtained in the first set of experiments anounced above. The slot is oriented downward and we compare what happens for a non-wetting and a wetting needle, decreasing the needle Weber number W0. At high W0 (i.e. W0>1) one observes respectively two well known wakes [2]: (a) a "hole" wake and (b) a sinuous wake, this last one being the equivalent of a Mach cone for sinuous waves. The opening angle
y of both wakes are identical, a fact discovered long ago by Lin [2]. In a way similar to what we said in section 1 for the stability criterion, this comes from the fact that the balance of momentum with surface tension in case (a) at the wake edge
is exactly equivalent to the Mach condition 
for case (b). Both arguments leads to the same angle given by 
. When reducing W0 , as appears on cases (b) and (c) of figure 2, the two wakes becomes clearly different. This is presumably due to the weight of liquid in case (c) accumulating at the edge of the wake that modifies the mechanical balance. Rather surprisingly, this effect does not change only the shape far from the needle (curvature of the wakes) but also the opening angle y.
(a) (b)
(c) (d)
(e) (f)
Figure 2: Response of the curtain to a needle for a 50 cP silicon oil, slot downward. (a) Non-wetting needle,
G = 1.54 cm2s-1, z0 =5 cm, W0 =3.5 ; (b) same values but with a wetting needle; (c) Non-wetting needle, G = 0.65 cm2s-1, z0=3.5 cm, W0=1.25; (d) same values, but with a wetting needle; (e) Non-wetting needle, G= 0.56 cm2s-1, z0=2.1 cm, W0=0.84; (f) Wetting needle, G= 0.57 cm2s-1, z0=3 cm, W0=1.01 .This indicates that measurements of surface tension performed via the opening angle of "hole wakes" must be taken with caution. The effect of the liquid weight becomes even more dramatic with a further decrease of W0. For W0 slightly smaller than 1, the sinuous wake disappears and is replaced by upstream sinuous wave propagation (fig. 2-e). On the contrary, the "hole wake" still exists with now a parabolic apex (
y=p/2).
Figure 3: Oscillations of a parabolic "hole wake" observed for
h=50 cP, G=0.51 cm2s-1, z0=1.92 cm, W0=0.73 (slot downward, wetting needle). Time between two pictures is 40 ms.
A liquid rim collecting the missing liquid edges the hole, this structure being similar to that of dry patches in films flowing down a slope studied in previous papers of our group [7].
Finally, a further decrease of W0 leads to a transition to a striking dynamical regime: surface tension finally dominates the other forces and the rim begins to move upward. Presumably, the rate of mass supplied to the rim increases. This one becomes heavier which reverses the motion before the rim "breaks" on the needle and becomes to detach from the curtain. Then, the upwards motion starts again and the system enters a periodic behaviour. This up to now unknown regime reveals again the essential role played in curtain stability by the rim weight, neglected in available studies.
In the second set of experiments, the slot has been turned upward. Reducing progressively the flow rate, just before break-up , we have observed a new instability reproduced on Figure 4. Sinuous undulations of the curtain are amplified which leads to the appearance of a "chessboard pattern" composed of two families of inclined waves travelling in opposite directions. The sinuous nature of this pattern has been checked by pictures taken from below (not reproduced here). Its striking spatial coherence comes from the fact that each inclined phase line travels as a whole, i.e. the wave velocity c* is constant everywhere in the curtain. This is really non trivial because the sinuous wave velocity 
depends on the position z. This means that, for unknown reasons, a particular velocity is selected and applies everywhere in the curtain.
We have performed extensive measurements of c* (and of the wavelength) and our data suggest that this velocity is very close to one half of the sinuous wave velocity c defined on the transonic line:
Figure 4: Chessboard instability of a liquid curtain observed in the following conditions: slot upward, tube diameter d=6 cm, viscosity
h=10 cP, flow-rate per unit length G=0.89 cm2s-1.
(1)
This result can be reached by dimensional analysis. It implies that everywhere in the curtain one has 
, which suggests a possible connection with problems of phase and group velocities. The theoretical origin of this curious result remains to be clarified.