1. IntroductionFluid Mechanics for graduate students
Non-Newtonian fluid mechanicsDelayed die swell
Luca Brandt & Christophe Duwig
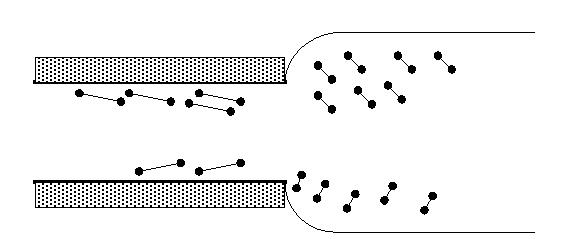
When a viscoelastic fluid is extruded from a pipe, the diameter of the
extruded jet usually increases, even to three or four times the diameter
of the pipe. At low rates of extrusion the swell appears to start at the
pipe exit. At high rates of extrusion the tendency of the jet to swell
at the exit is suppressed and there is a delay in the swell.
The die swell is a general phenomenon occurring in any viscoelastic
fluid and it is a very important problem in industry because so many processes
involve the extrusion of viscoelastic fluids, for example plastic in their
molten state. It was observed that delayed die swell is a critical phenomenon,
in the sense that it occurs beyond a critical speed of the fluid; this
is not so different than the wave speed of small perturbation in a viscoelastic
fluid ( think of it in analogy with the speed of sound in compressible
flows).
In fact, it may be shown that, if U, velocity of the fluid in the pipe,
is larger than the wave speed c, characteristic of the particular fluid,
the vorticity of flows perturbing Poiseuille flows of an upper convected
Maxwell model obeys an hyperbolic equation.
a) Die Swell
The phenomenon of die swell may be explained by elastic recovery. The molecules are stretched by the shear forces in the pipe and the average axial stress at the exit is a tension. The first normal stress difference, N1, is so fundamental to determine the actual elastic recovery and increase on the diameter of the jet once the shear stresses are removed outside the pipe. The die swell ratio is defined as the ratio of the maximum diameter of the jet and the diameter of the pipe.

2. Governing parameters
We introduce here the governing adimensional parameters with a short discussion.
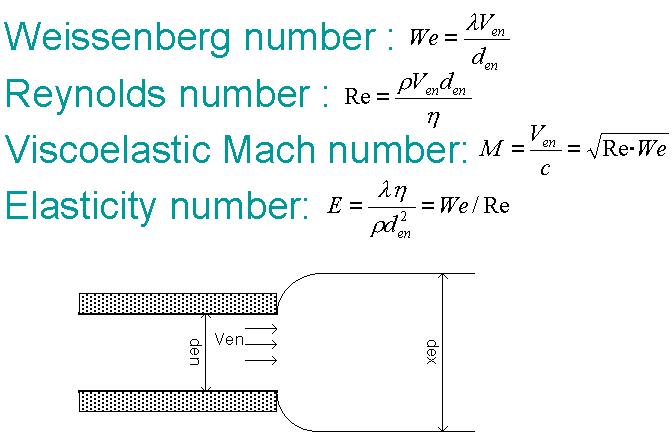
Two other parameters, which can be derived from these two, are considered
more relevant in the study of delayed die swell.
The viscoelastic Mach number, U/c, where c is the speed of shear waves
into a fluid at rest and the Elasticity number.
This is the ratio between the relaxation time and the viscous time
scale; it does not depend on the flow condition (inertia) but only on the
type of fluid and the experimental apparatus.
a) Speed of shear waves into a fluid at rest
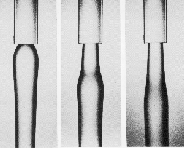
3. Experimental results
We present here shortly some conclusions from the experiments of Joseph
et al (1987).
For more pictures and details you can look at the slides
of our presentation.
4. Numerical investigations of the delay occurrence.
To understand the phenomenon, numerical simulations have been performed
by Delvaux & Crochet (1990). Due to numerical instabilities and difficulties,
the values of E (0.03-0.05) used in their computations are out of the range
of available experimental data (E>1.00).
Therefore, a validation by comparison with previous experiments is
not possible, but despite this restriction, the conclusions obtained from
the numerical simulations are fundamental to understand the physical mechanisms
involved in the phenomenon.
a) Inertia effects
The delay effect has been noticed when increasing the extrusion velocity. The influence of inertia is investigated by varying the Reynolds number. The figure below, figure 9 in the paper by Delvaux & Crochet (1990), shows the vorticity contour lines and the shape of the jet from two computations performed using an Oldroyd B model. The flow is assumed axisymmetric and only one half of a longitudinal section is displayed. In figure (a) Re=24.1 and We=0.7; in (b) the Reynolds number has been set to zero to eliminate inertia, while the Weissenberg number is kept constant. It is shown clearly that, without inertial effects, the swell occurs just after the pipe exit and no delay is observed. The vorticity varies almost linearly in the wall normal direction inside the pipe, but it changes immediately to zero outside because of the different boundary conditions (no shear stress). For a large enough value of Re instead, the vorticity in the middle of the jet results unaffected by the change in boundary conditions for a certain distance downstream and the swell is delayed. Therefore inertial effects are needed to understand delayed die swell phenomena.
b) Influence of elasticity
The influence of elasticity has also been investigated by Delvaux & Crochet(1990). Several calculations have been carried out keeping M constant above the critical value and varying E between 0.03 and 0.05. The Giesekus fluid model has been used and the results are reported in figure 13. The influence of the E on the position of the inflection point is noticed, i.e. it appears closer to the pipe exit for larger values. Note also that the swell ratio increases when E increases !
c) Information transmission
To investigate the influence of information transmission, the type of the governing partial differential equations is investigated. An Oldroyd B model has been used for these calculations. The dark areas in figure 6(c) correspond to the regions of hyperbolicity of the vorticity equation and different viscoelastic Mach numbers have been used to show the evolution of the delay. The finite elements meshes and the the stream function are also displayed in figure 6. Comparison between the streamlines and the filled zones shows that there is a close correspondence between the hyperbolic governed regions and the regions where delay is observed (no swell of the lines).
5. Conclusions
The following points are summarizing the (our) understanding on this phenomenon.
Question
34. Describe the die swell and delayed die swell phenomena, what are
the causes and which dimensionless numbers are used to describe them ?
Bibliography
Joseph D. D., Matta J. E., Chen K. 'Delayed die swell', J. Non-newtonian Fluid Mech 1987, 24:31,65.
Joseph D. D., 'Fluid Dynamics of Viscoelastic Liquids', Spinger 1990, Ch 13.
Delvaux V., Crochet M. J. 'Numerical simulations of delayed die swell', Rheologica Acta 1990, 29:1-10.
Joseph D. D., Christodoulou C. 'Independent confirmation that delayed die swell is a hyperbolic transition', J. Non-newtonian Fluid Mech 1993, 79:225,235.
Cloitre M., Hall T., Mata C., Joseph D. D. 'Delayed die swell and sedimentation of elongated particles in wormlike micellar solutions', J. Non-newtonian Fluid Mech 1998, 79:157,171.