RESEARCH
Flow control Stability and transition
On this page I give a brief introduction to my research activity, but it is still under construction so you are most welcome to revisit and read more at a later time.
| Flow control |
Delaying transition to turbulence by a passive mechanism |
|
|
Reducing skin friction is important in nature and in many technological applications. This reduction may be achieved by reducing stresses in turbulent boundary layers, for instance tailoring biomimetic rough skins. Here we take a second approach consisting in keeping the boundary layer laminar as long as possible by forcing small optimal perturbations. Due to the highly non-normal nature of the underlying linearized operator, these perturbations are highly amplified and able to modify the mean velocity profiles at leading order. We report results of wind-tunnel experiments in which we implement this concept by using suitably designed roughness elements placed on the skin to enforce nearly optimal perturbations. We show that using this passive control technique it is possible to sensibly delay transition to turbulence (Fig. 1). |
 Fig. 1 |
|
For further details see Phys. Rev. Lett. (2006), vol. 96, 064501. |
|
Flow around a porous cylinder subject to continuous suction or blowing |
|
|
In the present experimental investigation the surface pressure distribution, vortex shedding frequency, and the wake flow behind a porous circular cylinder are studied when continuous suction or blowingis applied through the cylinder walls. It is found that even moderate levels of suction/blowing(<5%of the oncoming streamwise velocity) have a large impact on the flow around the cylinder. Suction delays separation contributing to a narrower wake width, and a corresponding reduction of drag, whereas blowing shows the opposite behaviour. Both uniform suction and blowing display unexpected flow features which are analysed in detail. Suction shows a decrease of the turbulence intensity throughout the whole wake when compared with the natural case, whilst blowing only shows an effect up to five diameters downstream of the cylinder. The drag on the cylinder is shown to increase linearly with the blowing rate, whereas for suction there is a drastic decrease at a specific suction rate. This is shown to be an effect of the separation point moving towards the rear part of the cylinder, similar to what happens when transition to turbulence occurs in the boundary layer on a solid cylinder. The suction/blowing rate can empirically be represented by an effective Reynolds number for the solid cylinde, and an analytical expression for this Reynolds number representation is proposed and verified. Flow visualizations (Fig. 1) expose the complexity of the flow field in the near wake of the cylinde, and image averaging enables the retrieval of quantitative information, such as the vortex formation length. For further details see J. Fluids Struc. (2004), vol. 19, pp. 1031-1048. |
|
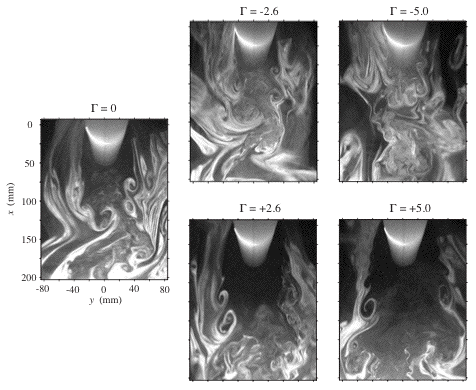 Fig. 1 | |
| Stability and transition |
Transition induced by free-stream turbulence |
|
|
Free-stream turbulence (FST) is perhaps the most important source inducing by-pass transition in boundary layer flows. The present study describes the initial energy growth of streamwise-oriented disturbances in the boundary layer originating from the presence of FST with intensities between 1.4% and 6.7%, but the study is mainly focused on the modelling of the transition zone. For this study three passive and one active turbulence-generating grids were used. The active grid was used in order to vary the turbulence intensity (Tu) without changing the setup in the test section. It is shown that the initial disturbance energy in the boundary layer is proportional to Tu². The experiments also show that the energy (E) grows in linear proportion to the Reynolds number based on the downstream distance (Fig. 1). Furthermore the transitional Reynolds number is shown to be inversely proportional to Tu² for the whole range of Tu studied (Fig. 2). The intermittency (γ) in the transitional zone was determined and it was shown that the intermittency function has a universal shape if the downstream distance is scaled with the length of the transition zone (Fig. 3). The Reynolds number based on this transition zone length was found to increase linearly with the transition Reynolds number; however it was also noted that this non-dimensional length has a minimum value. With these results we were able to formulate an expression for the spot production rate which has a better physical base than previous models. For further details see J. Fluid Mech. (2005), vol. 527, pp. 1-25. |
|
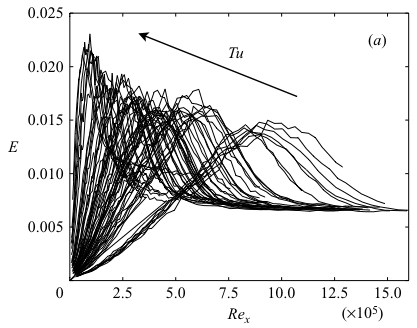 Fig. 1 |
|
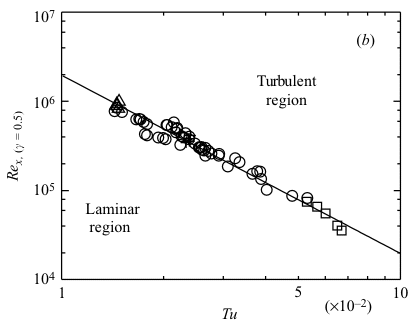 Fig. 2 |
|
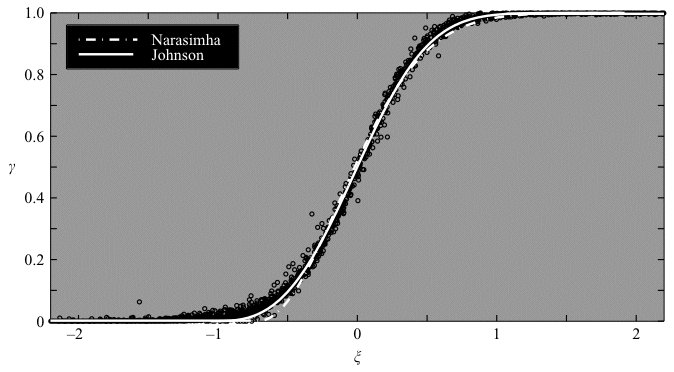 Fig. 3 |
|